huggingface.co - Tensor Parallelism (TP) in Transformers 5 Minutes to Understand

From Quentin Gallouédec:

Quick Recap: What’s Inside a Transformer Network?

Before diving into tensor parallelism, let’s briefly review the core components of a transformer model. We focus on two major components:

• the Multi-Head Attention (MHA) and
• the Feed-Forward Network (FFN)

Other components (layer norms, embeddings, etc.) are omitted here because tensor parallelism cannot be applied to them, and most of the model’s parameters reside in the Attention and FFN components anyway.

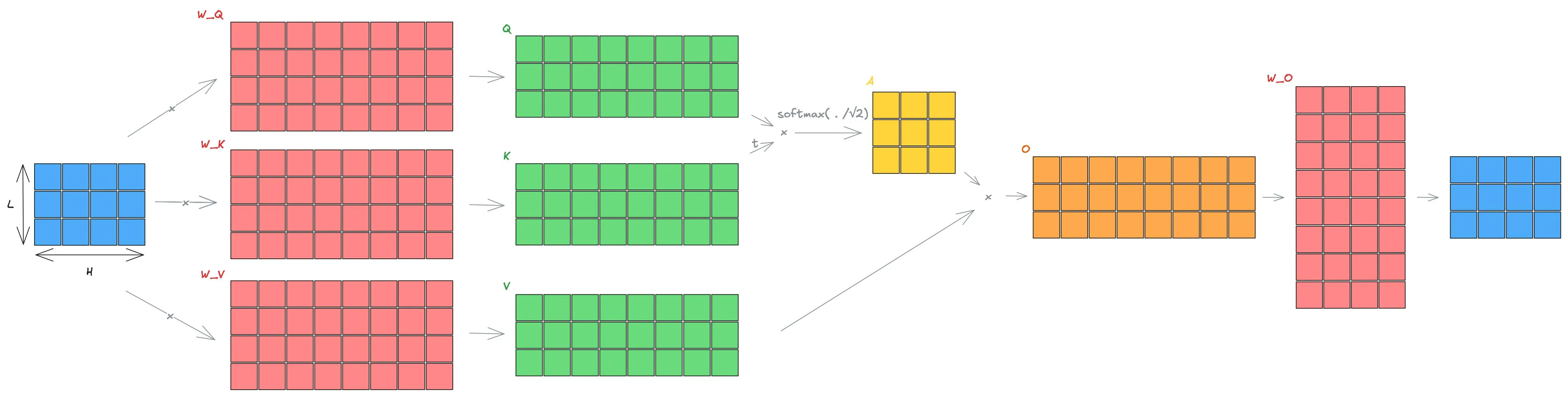
Attention

The backbone of transformer models is the attention mechanism. Although many variants exist (e.g., Multi-Query Attention, Grouped-Query Attention, Linear Attention), the formulation below is the standard one:

$$Attention(Q,K,V)=softmax(QK⊤d)V \boxed{ \text{Attention}(Q,K,V) = \text{softmax}\left(\frac{QK^\top}{\sqrt{d}}\right) V }$$

Here, the queries $Q Q$ , keys $K K$ , and values $V V$ are matrices of the same shape. In practice, they are obtained from the same input $X X$ (token embeddings) via learned linear projections:

$$Q=XWQ,K=XWK,V=XWV. Q = XW_Q,\quad K = XW_K,\quad V = XW_V.$$

A learned output projection $WO W_O$ then produces the final attention output:

$$Output=Attention(Q,K,V)WO. \text{Output} = \text{Attention}(Q,K,V) W_O.$$

Visually:

[

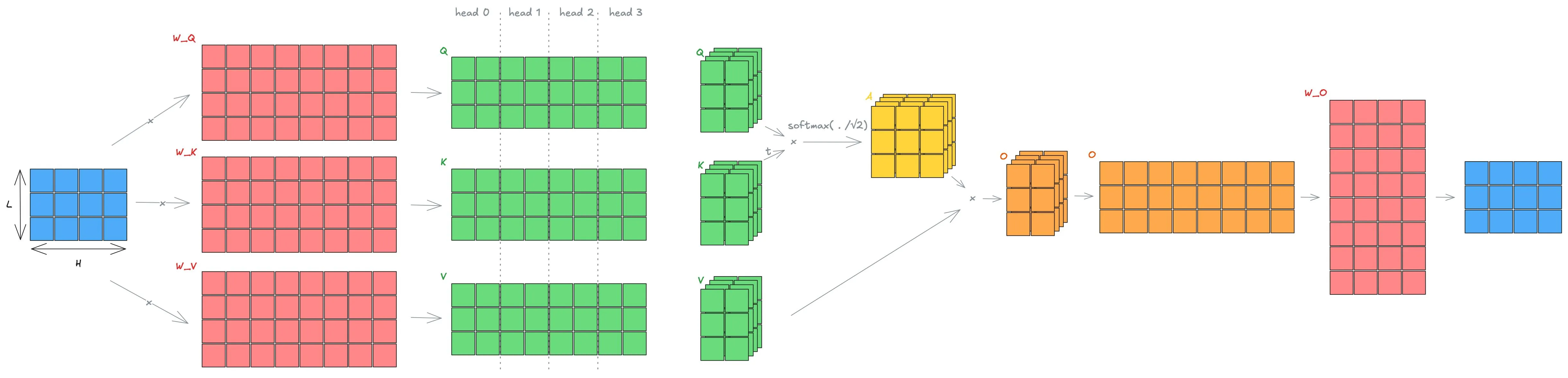
Multi-Head Attention

Computing attention with a large hidden dimension can be costly and may limit the model’s ability to capture diverse features. Transformers address this with Multi-Head Attention (MHA).

Instead of computing one large attention operation, we split $Q Q$ , $K K$ , and $V V$ into $h h$ smaller heads of dimension $dh=d/h d_h = d/h$ . Each head captures different representation subspaces. Their outputs are concatenated and projected back to dimension $d d$ , allowing the model to combine the information across heads.

[

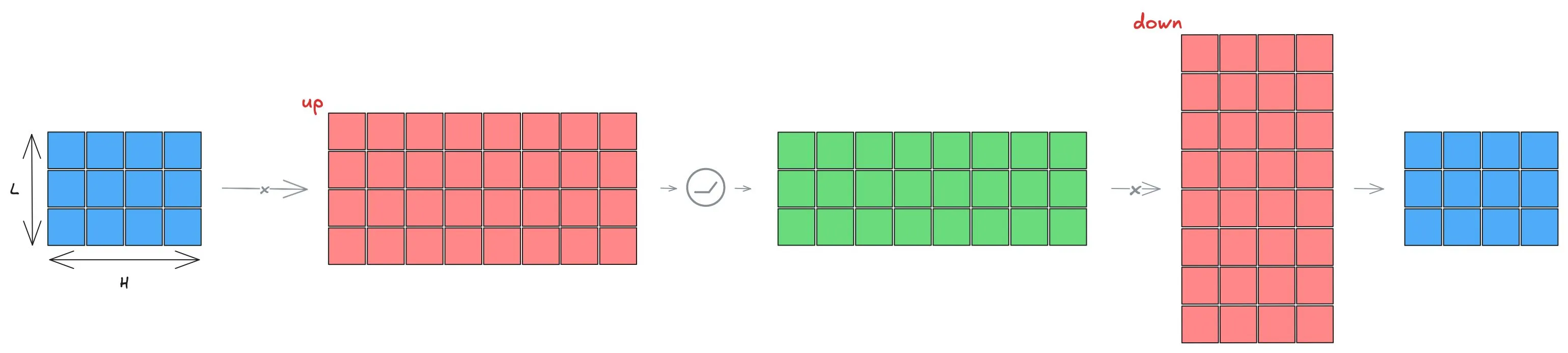
Feed-Forward Network (FFN)

Another crucial component is the Feed-Forward Network (FFN). It’s usually composed of two linear layers with an activation in between. Many variations exist, but let’s consider the common structure, as it generalizes well:

[

The Scaling Challenge

Transformer models have grown dramatically in size. Running inference on a single GPU is already challenging, and training is often impossible without parallelism. This motivates the need to split the model across multiple GPUs, which leads us to tensor parallelism, which is one of the key techniques enabling this.

What Is Tensor Parallelism?

Now that we remember how attention works, let’s put that aside for a moment and introduce Tensor Parallelism (TP).

The key idea is simple: matrix multiplications can be parallelized if we split the matrices in the right way. Suppose you need to compute a matrix multiplication and you have a friend to help. How should you divide the work?

[

One option is to split the second matrix into column blocks. Each person multiplies the full first matrix by one block of columns:

[

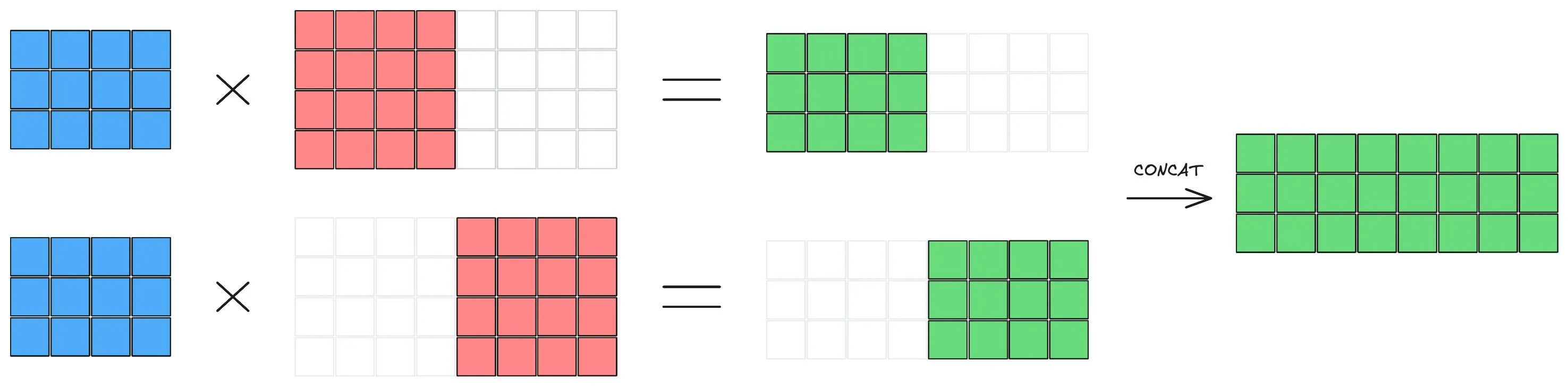
This is known as column-parallel matrix multiplication.

Another option is to split the first matrix into column blocks and the second matrix into matching row blocks. Each person computes their partial product, and then the results are summed:

[

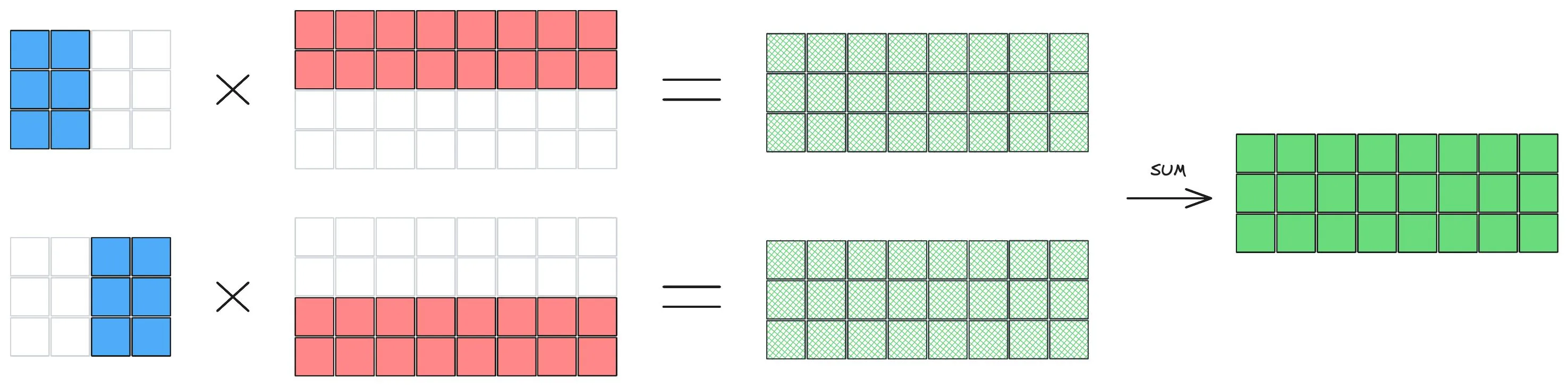
This is called row-parallel matrix multiplication.

These strategies are extremely useful: they let each worker operate independently on its shard of the data and, more importantly, allow us to distribute the matrices across multiple GPUs —precisely what is needed to reduce memory usage per GPU.

Tensor Parallelism in Attention

Now that we understand TP and MHA separately, let’s try to apply TP to MHA.

[

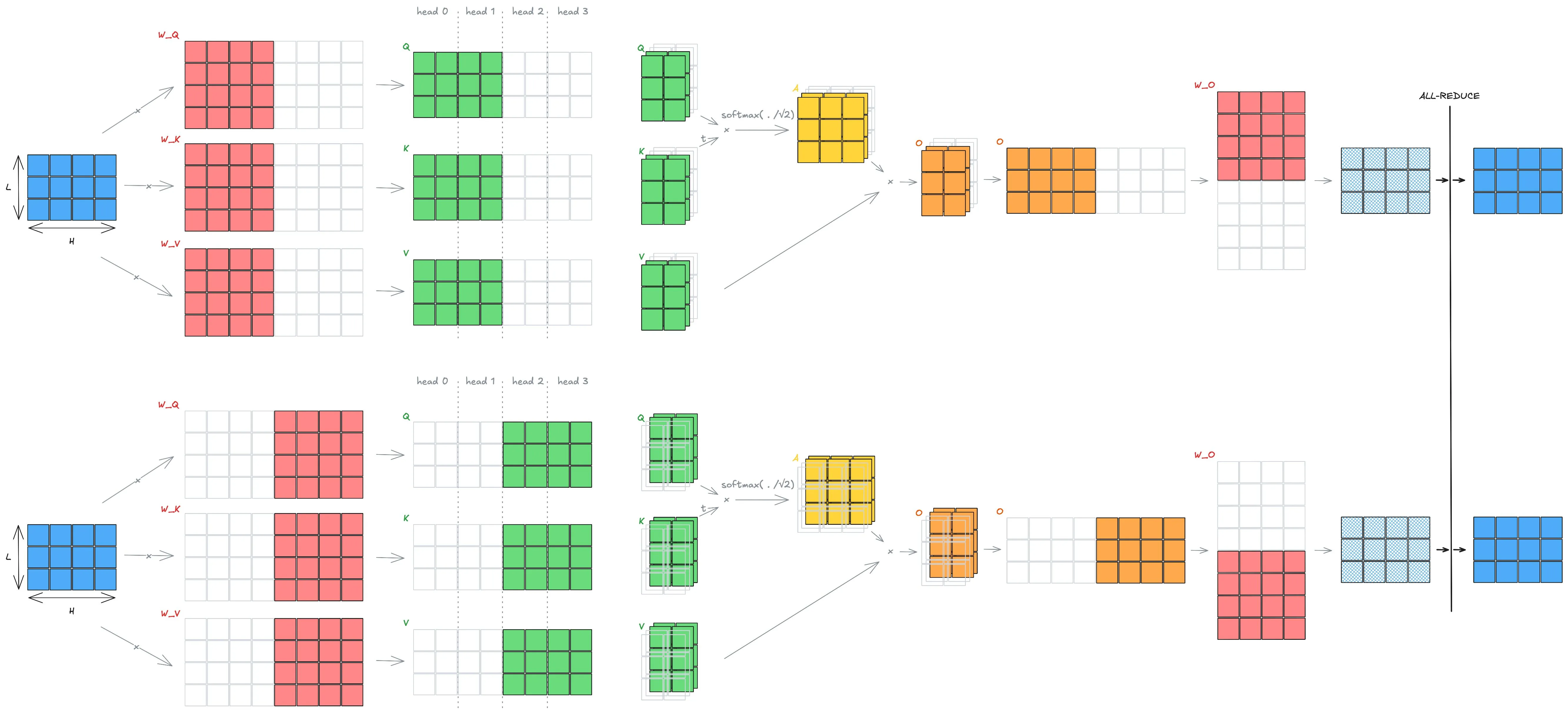
Splitting the Q, K, V Projections

The easiest way to do it is to split the projection matrices $WQ W_Q$ , $WK W_K$ , and $WV W_V$ column-wise. Each GPU holds a subset of the output dimensions—equivalently, a subset of the attention heads.

Each GPU therefore computes its local $Qi Q_i$ , $Ki K_i$ , and $Vi V_i$ for its assigned heads, with no communication required.

Local Attention Computation

Since heads are independent, every GPU can compute attention for its heads entirely locally:

• compute $QiKi⊤ Q_iK_i^\top$ ,
• apply softmax,
• multiply by $V V$ .

Once again, no communication is needed here.

The attention output $Oi O_i$ is thus naturally sharded by columns across GPUs.

Output Projection

The output projection $WO W_O$ is then applied using a row-parallel layout:

• each GPU multiplies its shard of the attention output by its shard of $WO W_O$ independently,
• then a single all-reduce (sum across GPUs) aggregates the partial results into the final output.

Tensor Parallelism in the Feed-Forward Network

Similarly, we can apply TP to the FFN in an even more straightforward way.

[

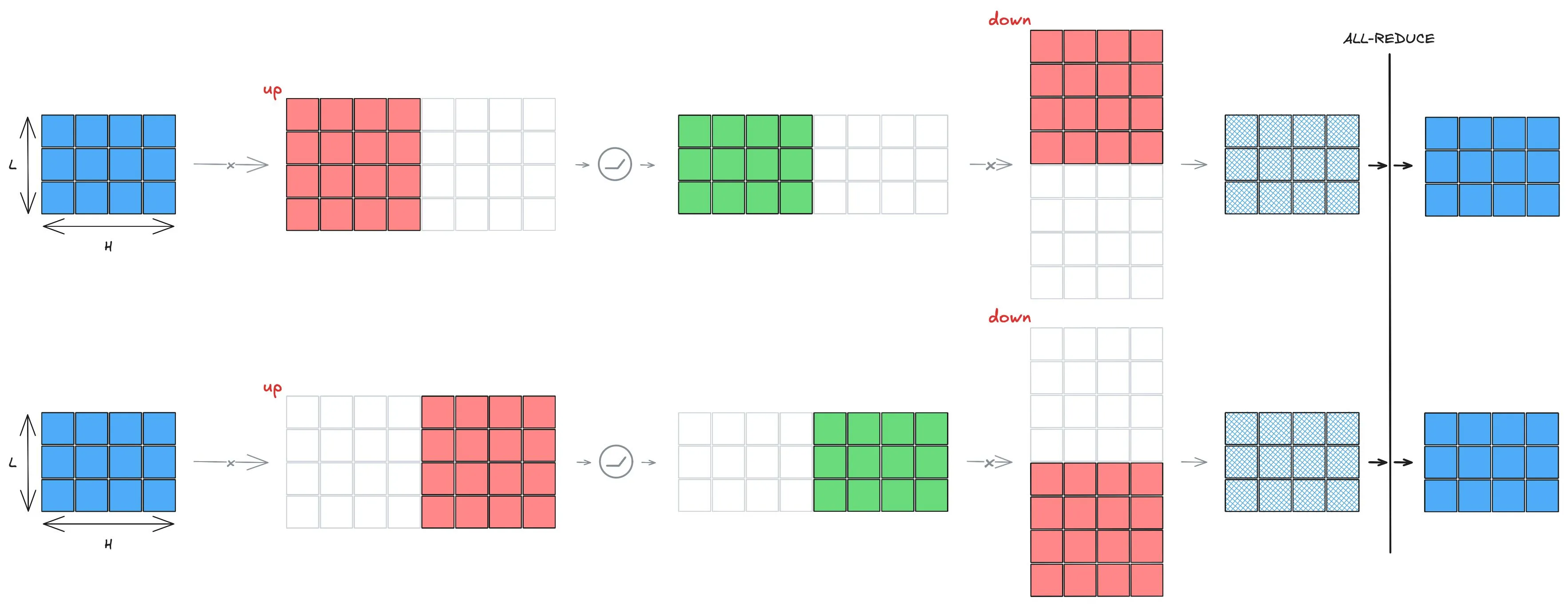
• The first linear layer is column-parallel.
• The second linear layer is row-parallel.

Some Constraints

Although this form of TP is elegant, it comes with a few practical constraints:

• The TP size (number of GPUs) must be less than or equal to the number of attention heads—a single head cannot be split across GPUs.
• The number of attention heads must be divisible by the number of GPUs, so each GPU receives an equal share of heads.
• The feed-forward hidden dimension must be divisible by the TP size, to ensure equal distribution of the FFN parameters.

TP in Practice

Now that we understand the theory, how to use TP in practice?

Fortunately, all transformer models integrated with the Hugging Face Transformers library can leverage TP via the tp_plan argument.

demo_tp.py

from transformers import AutoModelForCausalLM
import torch

model = AutoModelForCausalLM.from_pretrained("Qwen/Qwen3-8B", tp_plan="auto")
inputs = torch.tensor([1, 2, 3, 4](1,%202,%203,%204), device="cuda")
outputs = model(inputs)

torchrun --nproc_per_node 4 demo_tp.py

Read more about how to customize the TP plan in the Transformers’ documentation – Distributed inference.

What TP Doesn’t Solve

While TP efficiently distributes large matrix multiplications, it does not solve all challenges of training or serving large models. Its scalability is limited by the number of attention heads, and because TP requires frequent communication between GPUs, performance can degrade across multiple nodes where inter-node bandwidth is lower. To overcome these limitations, additional forms of parallelism—such as Pipeline Parallelism (PP)—are needed. We’ll explore these techniques in future sections!

Community

ArthurZ

model = AutoModelForCausalLM.from_pretrained("Qwen/Qwen3-8B", tp_plan="auto") damn simple!